acwing算法笔记-前缀和与差分

前缀和

前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和。它是一种重要的预处理，能大大降低查询的时间复杂度。

这里，我们把前缀和问题大致分为一维前缀和与二维前缀和。

一维前缀和

---

这里直接看一道一维前缀和的模板题，方便更好地分析。

暴力解法

这里很容易直接想到暴力解法，遍历区间求和。

int sum = 0;
for( int i = L; i <= R; i++ )   sum += a[i];

对于单次查询，时间复杂度很容易看出为O(n),这里有m次查询，所以程序的时间复杂度为O(n*m)。

如果n和m的数据量稍微大一点就有可能超时，而我们如果使用前缀和的方法来做的话就能够将时间复杂度降到O(n+m),大大提高了运算效率。其中对于单次查询，区间求和的时间复杂度减小到O(1)。

基本思想

1. 预处理前缀和数组
其实也就是问S[i]该如何计算
首先做一个预处理，定义一个前缀和数组S[]，S[i]代表原数组中前i个数的和。

// 计算前缀和数组的时间复杂度为O(n)
for (int i = 1; i <= n; i++ ) s[i] = s[i - 1] + a[i];

2. 用公式求区间和

// 对于每次查询，只需执行sum[r]-sum[l-1] ，时间复杂度为O(1)
sum[l, r] = sum[r] - sum[l - 1]

证明如下：
$sum[r] =a[1]+a[2]+a[3]+a[l-1]+a[l]+a[l+1]……a[r];$
$sum[l-1]=a[1]+a[2]+a[3]+a[l-1];$
$sum[r]-sum[l-1]=a[l]+a[l+1]+……+a[r]$

代码模板

#include <iostream>
using namespace std;

const int N = 100010;

int n, m;
int a[N], s[N];

int main()
{
    scanf( "%d%d", &n, &m );

    // a[0] == 0，下标从 1 开始输入
    for( int i = 1; i <= n; i++ ) scanf("%d", &a[i]);

    // s[0] == 0，下标从 1 开始计算
    for( int i = 1; i <= n; i++ ) s[i] = s[i - 1] + a[i]; // 计算前缀和

    while( m-- )
    {
        int l, r;
        scanf( "%d%d", &l, &r );
        printf( "%d\n", s[r] - s[ l - 1 ] ); // 区间和的计算 
    }
    return 0;
}

注意事项

原数组与前缀和数组下标从1开始

• 由于计算区间和的公式是s[r] − s [l−1],如果实际存数的区间从0开始，那么0 − 1就越界了，所以前缀和数组最开头要放一个0，实际存数的区间是[1, n]。
• 统一区间内求和的公式，便于理解，即前x个数的和为S[x]，第x个数的下标为x。

Reference

[1]. 前缀和 【c++详细题解】
[2]. Bug-Free

二维前缀和

---

二维前缀和相比于一维前缀和略微复杂一些，这里同样给出模板题，便于分析。

暴力解法

int sum = 0;
for( int i = x1; i <= x2; i++ )
    for( int j = y1; j <= y2; j++ )
        sum += a[i][j];

与一维前缀和暴力求解类似，使用双重循环直接求解，每次查询的时间复杂度为$O(nm)$，但使用前缀和求解，每次查询的时间复杂度为$O(1)$.

基本思想

大体思路与一维前缀和模板相同，但是这里预处理前缀和数组，以及求区间和的公式稍微要复杂一些。这里给出相应的图帮助理解。

1. 预处理前缀和数组
其实也就是问$S[i, j]$该如何计算

这里先给出前缀和S[x][y]的定义，x为行坐标，y为列坐标（这里x,y不是横纵坐标！）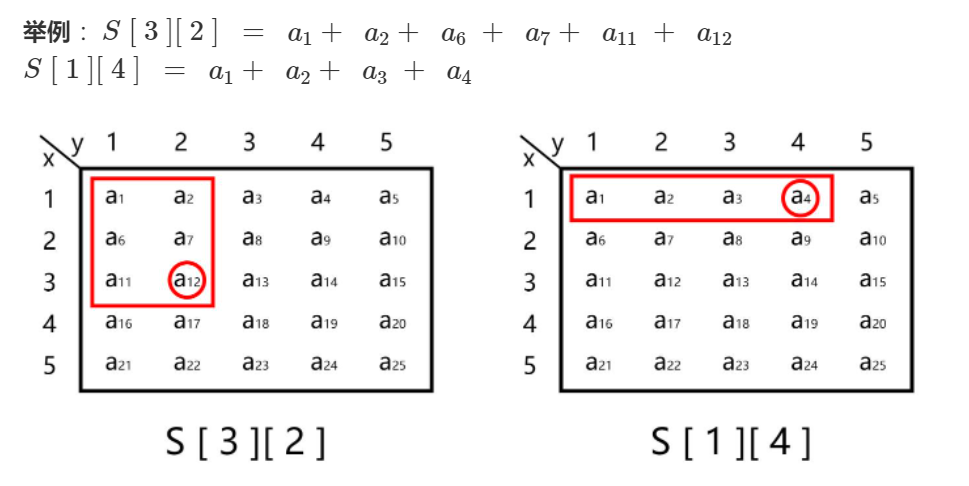

前缀和$S[i, j]$的计算公式
$S[i][j] = S[i][j - 1] + S[i - 1][j] - S[i - 1][j - 1] + a[i][j]$

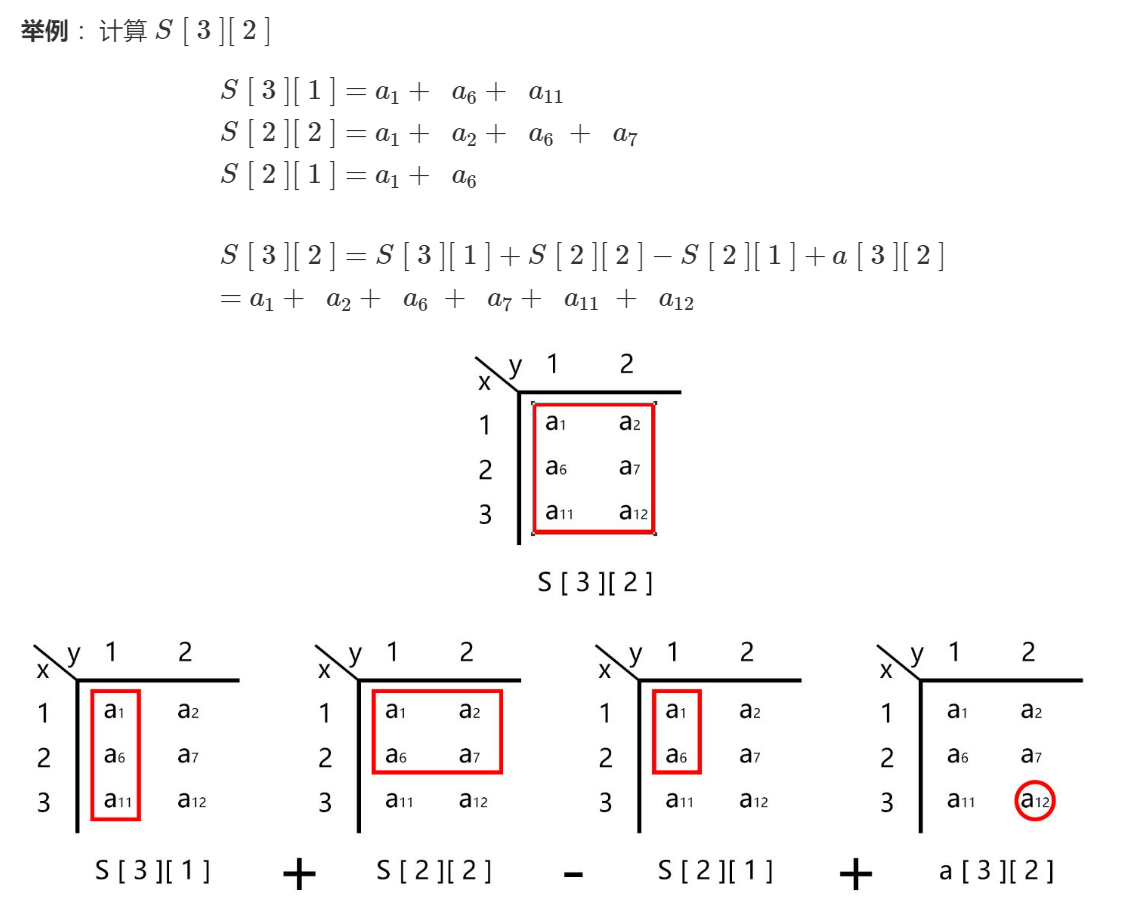
2. 用公式求区间和
求(x1, y1), (x2, y2)子矩阵中的和
$Sum = S[x_2][y_2] - S[x_2][y_1 - 1] - S[x_1 - 1][y_2] + S[x_1 - 1][y_1 - 1]$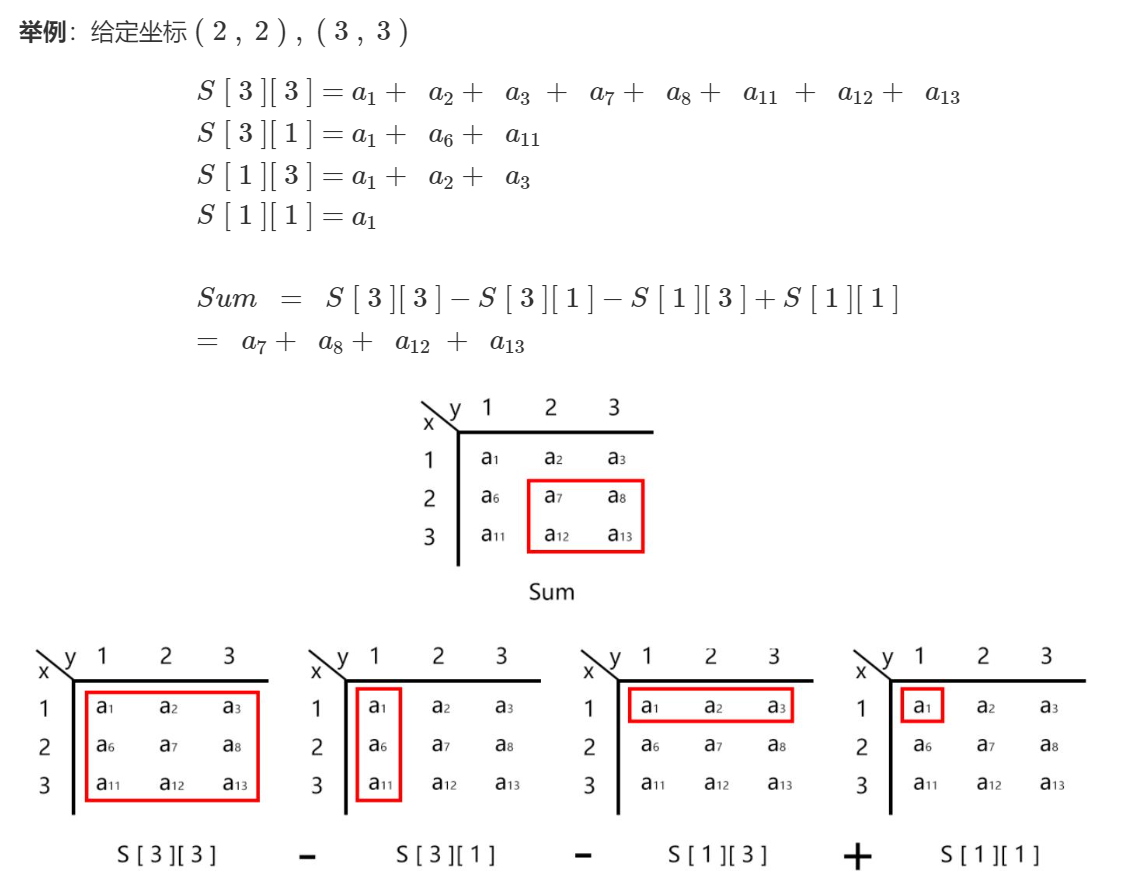

代码模板

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    // a[0][0] == 0，下标从 a[1][1] 开始输入
    for(int i =1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);

    // s[0][0] == 0，下标从 s[1][1] 开始计算
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            // 计算二维前缀和 
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; 

    while(q--)
    {
        int x1, y1, x2, y2;
        scanf( "%d%d%d%d", &x1, &y1, &x2,&y2 );
    // 计算子矩阵的和 
        int sum = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]; 
        printf( "%d\n", sum );
    }
    return 0;   
} 

注意事项

输入数据和计算前缀和时，下标从 1 开始。

差分

类似于数学中的求导和积分，差分可以看成前缀和的逆运算。对于一个数组$a$，其差分数组$b$的每一项都是$a[i]$和前一项$a[i−1]$的差，即$b[i]=a[i]−a[i−1]$。

同样地我们这里也将差分问题大致分为一维差分和与二维差分问题。

一维差分

---

这里直接给出模板题，方便论述。

暴力解法

for (int i = l; i <= r; i++ ) 
    a[i] = a[i] + c

对于单次操作，时间复杂度很容易看出为O(n),这里有m次操作，所以程序的时间复杂度为O(n*m)。

如果n和m的数据量稍微大一点就有可能超时，而我们如果使用差分的方法来做的话就能够将时间复杂度降到O(n+m),大大提高了运算效率。其中对于单次操作，时间复杂度减小到O(1)。

基本思想

为了方便理解我们这里给出三个数组，原数组a[], 前缀和数组s[], 差分数组b[]。
前缀和和差分是一个互逆的关系，a[]是s[]的差分数组，b[]的前缀和数组

首先我们回顾一下前缀和数组s的性质，对于原数组a，只要给某个数加上x，那么后面所有的数在求前缀和数组s的时候都会被加上x。同理差分数组b只要给某个数加上x，那么后面所有的数在求原数组a的时候都会被加上x

根据这个性质，在原数组a的(l, r)区间内加上一个数可以用b[l] += x, b[r + 1] -= x来实现，让数组从l开始到最后都加上x，但超出r的范围也加上了x，所以我们需要让r后面的都减去x，保持原来的值。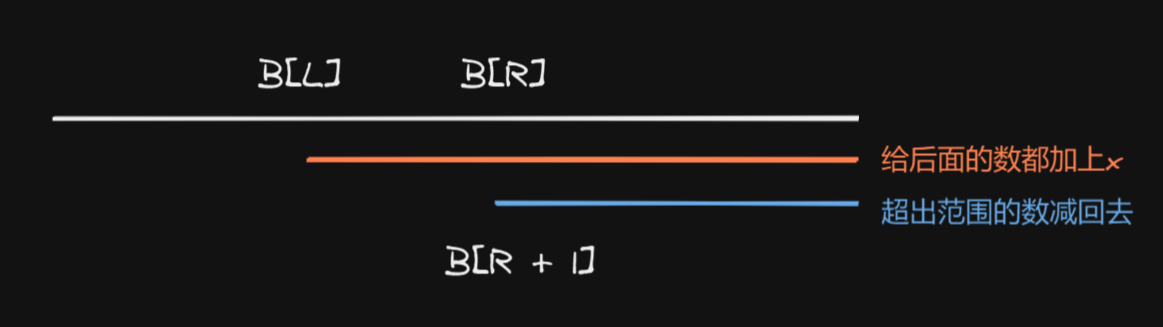

1. 预处理差分数组
其实也就是问b[i]该如何计算
$b[i] = a[i] - a[i - 1]$

2. 差分核心操作
给a数组中的[l, r]区间中的每一个数都加上c,只需对差分数组b做b[l] += c, b[r+1] -= c

3. 还原原数组
对差分数组求前缀和，还原原数组。

代码模板

#include<iostream>

using namespace std;

const int N=1e5+10;
int a[N],b[N];

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) 
    {
        scanf("%d",&a[i]);
        b[i]=a[i]-a[i-1];      //构建差分数组
    }

    int l,r,c;
    while(m--)
    {
        scanf("%d%d%d",&l,&r,&c);
        b[l]+=c;     //表示将序列中[l, r]之间的每个数加上c
        b[r+1]-=c;
    }

    for(int i=1;i<=n;i++) 
    {
        a[i] = a[i-1] + b[i];  //求前缀和运算
        printf("%d ",a[i]);
    }
    return 0;
}

注意事项

• 从数学角度来讲，差分数组更改了，原数组会自动更新，但这里的代码的角度构造的时候两个数组本没有时时联动关系，对差分数组操作以后需要通过手动更新原数组
• 原数组和差分数组下标都是从1开始

Reference

[1]. 差分 【c++详细题解】

二维差分

---

二维差分相比于一维差分略微复杂一些，这里同样给出模板题，便于分析。

暴力解法

int sum = 0;
for( int i = x1; i <= x2; i++ )
    for( int j = y1; j <= y2; j++ )
        a[i][j] += c;

与一维差分暴力求解类似，使用双重循环直接操作，每次操作的时间复杂度为$O(nm)$，但使用差分，每次操作的时间复杂度可以降低为$O(1)$.

基本思想

同样的三步走
1. 预处理差分数组
这里构造差分数组不像一维差分那么容易，所以我们这里直接用$insert()$的方式在每个位置$(i,j) → (i,j)$（指左上角是$(i,j)$，右下角也是$(i,j)$的子矩阵）插入值$a[i][j]$就可以了。

其实也可以通过前缀和公式逆运算，构造差分数组，因为第三步还原原数组肯定会用到前缀和公式，所以很容易逆推出差分数组的公式。

2. 差分核心操作
设A(x1, y1)为需要加值的子矩阵的左上角，B(x2, y2)为需要加值的子矩阵的右下角。
给(x1, y1), (x2, y2)子矩阵中每个数加上c。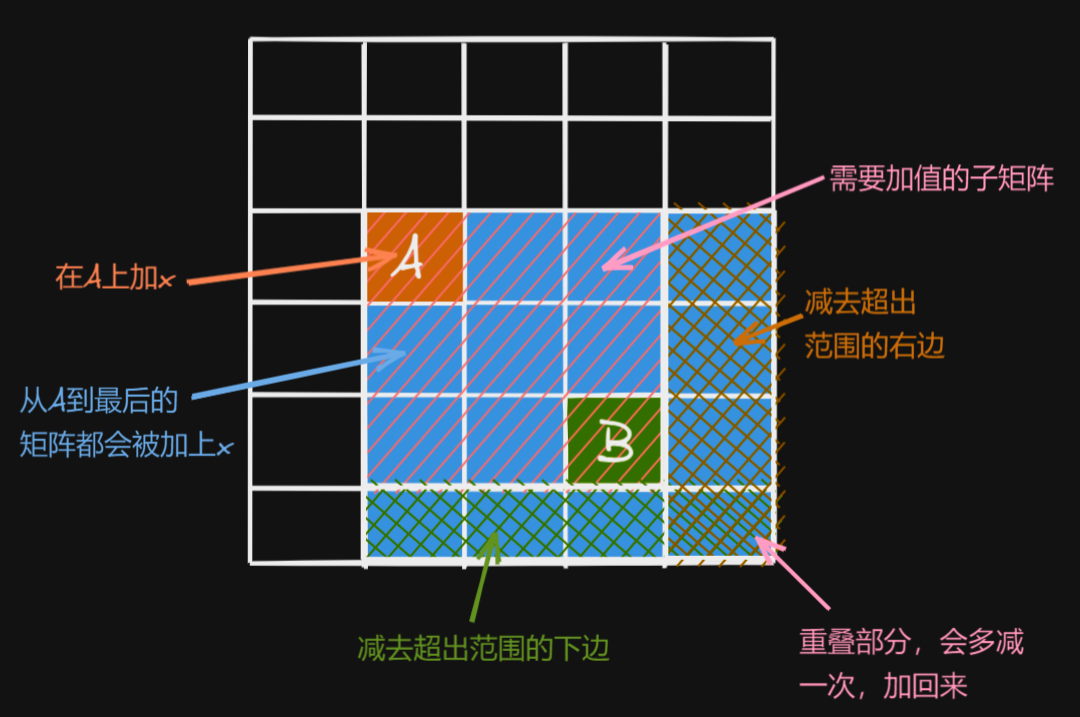

B[x1][y1] += x; //给A到最后的矩阵加x
B[x1][y2 + 1] -= x; //减去超出范围的右边
B[x2 + 1][y1] -= x; //减去超出范围的下边
B[x2 + 1][y2 + 1] += x; //把重复删减的部分给加回来

然后将上述操作封装为一个insert函数，来方便构建差分数组。

3. 还原原数组
这里要利用二维前缀和计算公式，还原原数组

代码模板

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);

    //构造差分数组
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            insert(i, j, i, j, a[i][j]);

    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        //差分核心操作
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ )
        {
            //前缀和运算，还原原数组
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
            printf("%d ", a[i][j]);
        }
        //换行
        puts(" ");
    }    
    return 0;
}

Reference

[1]. 差分矩阵