acwing算法笔记-双指针

双指针算法

本质：
双指针算法顾名思义就是要维护两个指针，这两个指针可能指向同一个序列当中的不同位置，也有可能指向不同的序列。但其本质就是利用单调性缩减枚举空间


暴力枚举

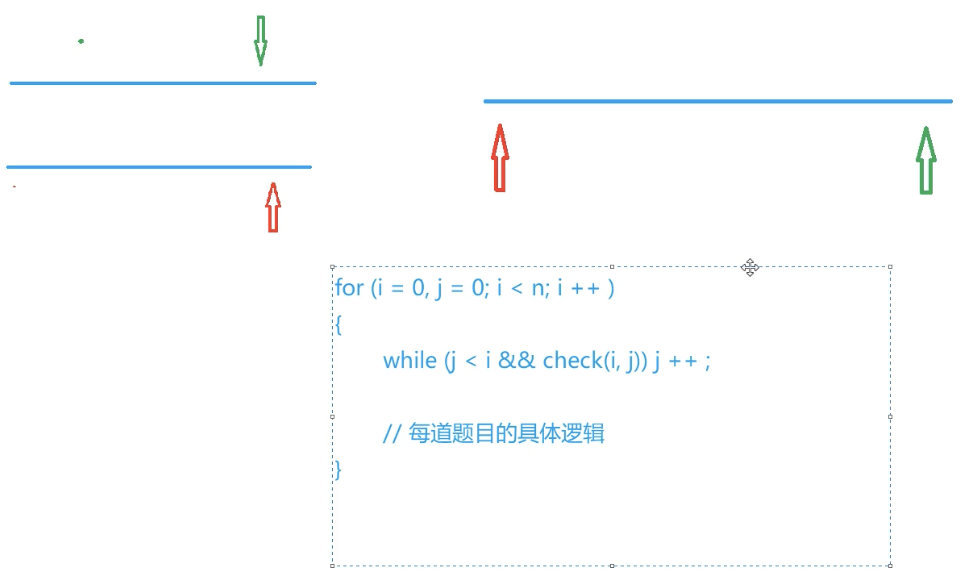
枚举一个指针，找另一个合法的指针，这里check指的是维护合法性质（根据题目条件判定，简单来说while不合法移动指针到合法为止，这样就找到了合法的另一个指针）

两个指针的位置的排列组合有$n^2$种，相应的时间复杂度也是$O(n^2)$，但如果应用双指针算法，可以将时间复杂度降至$O(n)$：比如说两个指针不回退扫描同一个序列，每一个指针在上图所有的循环里面总共移动的次数是不超过n的，我们可以应用某些单调的性质实现这一点。快速排序，归并排序，KMP算法本质上都是双指针算法。

双指针算法的解题思路大概是这样：暴力枚举->分析两个指针之间的单调性（探索有没有可能一个指针随着另一个指针的变化而变化）->通过单调性将暴力解法的时间复杂度降低一维

注意事项：

  1. 如果双指针指向一个序列，那么while里的另一个指针的条件就是指针相遇之前
  2. 如果双指针指向两个序列，那么while里的另一个指针的条件就是不越界
  3. 分析的时候合法条件可以分离出一部分处理，例如移动这种条件

799. 最长连续不重复子序列

基本思路

  1. 双指针问题一般可以先从暴力做法开始思考，对于上述问题，可以暴力枚举子串的起点和终点

    1
    2
    3
    4
    for (int i =0, j =0; i < n; i ++)
        for (int j  = 0; i <= i; j ++)
            if (check(j, i)) //合法 满足最长不重复子串性质
                res = max(res, i - j + 1); //对于所有i的最长不重复子串 找到最长的

  2. 分析i和j是否存在单调性

首先i是指向子串终点的指针，枚举i指针，我们去找合法的j指针（这里的合法也就是最长不重复子串）：在每次迭代中，我们让i往后移一个位置，随着i往后移动，j只能随之一起向后移动，不可能往前移动（因为要维护最长不重复子串合法，可以反证法证明）

因此，我们发现了双指针存在单调性，可以优化枚举空间，优化后的伪代码如下：

1
2
3
4
for(int i=0, j=0; i<n; i++) {
    while(j<=i && check(j, i)) j++;
    res = max(res, i-j+1);
}

这个算法当中，i和j两个指针它们只会加起来最多移动2n次，因此时间复杂度降到了O(n)

所以说双指针算法本质上就是要发现朴素算法中的一些性质，尤其是单调性，让我们由需要枚举n^2个状态变成需要枚举n个状态

注意：

  1. 哈希表维护的区间，如果value是次数，一般我们可以直接数组模拟哈希表更方便
  2. 如果用unordered_map模拟的话，如果维护次数用的是key，那我们统计key用count函数，变化key用erase函数；
    如果维护次数用的是value，那我们统计用hash[k],变化value就是变化hash[k]
    不管是用key还是用value，对于插入操作，insert函数和hash[k]变化效果一样
  3. 大数组要开在全局下，不能开在main等其他函数中，否则会爆栈

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>

using namespace std;

const int N = 100010;

int n;
int q[N], s[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    int res = 0;
    for (int i = 0, j = 0; i < n; i ++ )
    {
        s[q[i]] ++ ;
        while (j < i && s[q[i]] > 1) s[q[j ++ ]] -- ;
        res = max(res, i - j + 1);
    }

    cout << res << endl;

    return 0;
}

Reference

[1]. yxc


800. 数组元素的目标和

基本思路

暴力枚举两个数时间复杂度$O(n^2)$所以想办法优化，这里发现了指针之间的单调性，所以可以用双指针优化，然后这里是反向双指针
题目很简单，这里就注意两点

  1. 因为是反向双指针，所以其实位置是两侧
  2. 我们双指针算法找到的是对于每一个i的合法方案，这里的合法不能写a[i] + b[j] == x，因为不是每一个i都会有这种方案存在，
    但是起初的时候i指向0，所以一定满足是所有i里最小的，再加上一定有解，所以合法条件是a[i] + b[j] <= x

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m, x;

int a[N], b[N];

int main()
{
    cin >> n >> m >> x;
    
    for (int i = 0; i < n; i ++ ) cin >> a[i];
    for (int i = 0; i < m; i ++ ) cin >> b[i];
    
    for (int i = 0, j = m - 1; i < n; i ++) {
        while (j >= 0 && a[i] + b[j] > x) j--;
        if (a[i] + b[j] == x) cout << i << ' ' << j << endl;
    }
    
    return 0;
}

Reference

[1]. yxc

2816. 判断子序列

基本思路

这题很明显可以用暴力解法求解，枚举a[]里的数，然后对于每一个数扫描一遍b[]看是否在里面，时间复杂度显然是$O(n^2)$,所以我们尝试优化。
这里发现指针之间的单调性，假设i指向a数组，j指向b数组，对于当前i我们找到了合法的j，如果i后移，因为要保证子序列按原有次序排序，所以j也只能往后移，发现单调性，可以用双指针算法优化。

注意这里合法的j实际上是有两个条件 1. 值相同 2. 并且j至少移动一位，代码实现就是a[i] = b[j] and j > 上一层的j, 在这里大于上一层的j不是很好拿到。
所以我们把j至少移动一位的条件分离了出来，这样更容易实现。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int a[N], b[N];

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++ ) cin >> a[i];
    for (int i = 0; i < m; i ++) cin >> b[i];
    
    for (int i = 0, j = 0; i < n; i ++ ) {
        while (j < m && a[i] != b[j]) j++;
        // cout << i << " " << j <<  endl;
        if (j > m - 1) {
            cout << "No";
            return 0;
        }
        else j++;
    }
    cout << "Yes";
}

Reference

[1]. 判断子序列


相关题目

LeetCode 3. 无重复字符的最长子串
LeetCode 167. 两数之和 II - 输入有序数组

算法 > AcWing
#算法 #双指针
acwing算法笔记-双指针
https://vendestine.com/two-pointer
Author
Wenzhe Li
Posted on
March 29, 2022
Licensed under